Часть II
Новая физика, необходимая для понимания разума. В поисках невычислительной физики разума
5. Структура квантового мира
5.12. Гильбертово пространство
Чтобы более внятно (и более точно) рассказать о том, как работает процедура R в стандартных квантовомеханических описаниях, необходимо перейти на несколько (совсем немного) более высокий уровень математической абстракции. Семейство всех возможных состояний квантовой системы образует так называемое гильбертово пространство. Нужды объяснять значение этого термина во всех математических тонкостях у нас в данный момент нет, однако некоторое представление о нем все же получить стоит — это поможет нам прояснить существующую картину квантового мира.
Первая и наиболее важная особенность, на которую следует обратить внимание: гильбертово пространство является комплексным векторным пространством. Это, в сущности, означает, что здесь мы вправе выполнять действия с комплексно-взвешенными комбинациями, посредством которых описываются квантовые состояния. Для обозначения элементов гильбертова пространства я продолжу использовать диракову скобку «кет», т.е. если состояния |ψ〉 и |φ〉 являются элементами гильбертова пространства, то таким же его элементом является и состояние w|ψ〉 + z|φ〉, где w и z — любая пара комплексных чисел. Допускается даже комбинация w = z = 0, она дает элемент 0 гильбертова пространства — единственный элемент, не соответствующий никакому возможному физическому состоянию. Как и в любом другом векторном пространстве здесь действуют самые обыкновенные алгебраические правила:
|ψ〉 + |φ〉 = |φ〉 + |ψ〉,
|ψ〉 + (|φ〉 + |χ〉) = (|ψ〉 + |φ〉) + |χ〉,
w(z|ψ〉) = (wz)|ψ〉,
(w + z)|ψ〉 = w|ψ〉 + z|ψ〉,
z(|ψ〉 + |φ〉) = z|ψ〉 + z|φ〉,
0|ψ〉 = 0,
z0 = 0,
а это более или менее означает, что мы можем использовать алгебраическую систему обозначений привычным нам образом.
Иногда гильбертово пространство имеет конечную размерность — как, например, при описании спиновых состояний частицы. В случае спина 1/2 гильбертово пространство двумерно, а его элементы представляют собой комплексные линейные комбинации двух состояний, |↑〉 и |↓〉. Для спина 1/2 n гильбертово пространство (n + 1)-мерно. Однако размерность гильбертова пространства может быть и бесконечной — такое пространство необходимо, например, для описания состояний положения частицы. В этом случае каждое альтернативное положение, которое может занимать частица, рассматривается как отдельное измерение гильбертова пространства. Общее же состояние, определяющее квантовое местоположение частицы, записывается как комплексная суперпозиция всех этих различных отдельных положений (волновая функция для данной конкретной частицы). Надо сказать, что с рассмотрением такого бесконечномерного гильбертова пространства связаны определенные математические осложнения, которые лишь запутают нас без всякой на то необходимости, поэтому ниже я сосредоточусь (в основном) на конечномерном случае.
Попытавшись представить гильбертово пространство визуально, мы сталкиваемся с двумя трудностями. Во-первых, размерность такого пространства, как правило, слишком велика для того, чтобы наше воображение сколько-нибудь адекватно справилось с задачей. Во-вторых, пространство это является не вещественным, но комплексным. Впрочем, часто бывает полезно не задумываться о подобных трудностях с самого начала — это помогает выработать некоторое интуитивное понимание математических аспектов концепции. Поэтому давайте на некоторое время сделаем вид, будто для представления гильбертова пространства вполне достаточно той привычной двух- или трехмерной картины, которая у нас уже есть. На рис. 5.22 проиллюстрирована геометрически операция линейной суперпозиции на примере обычного трехмерного пространства.
Рис. 5.22. Если вообразить, что гильбертово пространство тождественно трехмерному евклидову пространству, то сумму векторов |ψ〉 и |φ〉 можно найти с помощью обычного правила параллелограмма (в плоскости (0, |ψ〉, |φ〉).
Вспомним, что вектор квантового состояния |ψ〉 соответствует тому же физическому состоянию, что и любой кратный ему вектор u|ψ〉, где u — ненулевое комплексное число. В нашей геометрической интерпретации это означает, что физическое состояние представляется не одинокой точкой в гильбертовом пространстве, но прямой, соединяющей гильбертову точку |ψ〉 с началом координат 0 (такую прямую называют лучом). Пример луча изображен на рис. 5.23; следует, впрочем, учитывать, что ввиду комплексного характера гильбертова пространства луч этот только выглядит как обычная одномерная прямая, на деле же за ним скрывается целая комплексная плоскость.
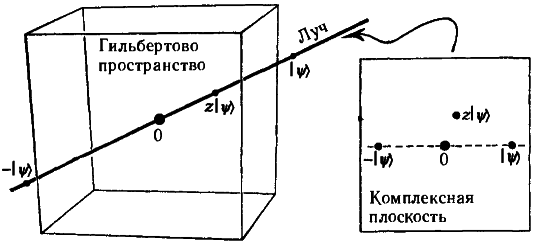
Рис. 5.23. Луч в гильбертовом пространстве есть множество всех комплексных кратных вектора состояния |ψ〉. Мы представляем этот луч в виде прямой, проходящей через начало гильбертовых координат, однако не следует забывать о том, что за этой прямой на деле скрывается комплексная плоскость.
До сих пор мы рассматривали гильбертово пространство, имея в виду лишь то, что структурно оно представляет собой комплексное векторное пространство. Однако, помимо комплексно-векторной структуры, у гильбертова пространства имеется еще одно, не менее важное, свойство, крайне полезное для описания процедуры редукции R. Речь идет об эрмитовом скалярном произведении (или внутреннем произведении), каковая операция позволяет из любой пары гильбертовых векторов получить одно-единственное комплексное число. Она же дает нам возможность ввести два весьма важных понятия. Первое — квадрат длины гильбертова вектора как скалярное произведение вектора на самого себя. Например, нормированное состояние (необходимое, как мы отмечали выше — см. §5.8, — для строгой применимости правила квадратов модулей) задается гильбертовым вектором, квадрат длины которого равен единице. Вторым важным понятием, сопутствующим скалярному произведению, является понятие ортогональности гильбертовых векторов — векторы ортогональны, когда их скалярное произведение равно нулю. Ортогональными считаются векторы, направленные, в том или ином смысле, «под прямым углом» друг к другу. Применительно к состояниям, ортогональными обычно называют состояния, независимые одно от другого. Важность этого понятия для квантовой физики заключается в том, что различные альтернативные результаты любого измерения всегда ортогональны друг другу.
В качестве примера ортогональных состояний можно привести состояния |↑〉 и |↓〉, с которыми мы встречались при рассмотрении частицы со спином 1/2. (Отметим, что ортогональность в гильбертовом пространстве, как правило, не соответствует перпендикулярности в пространстве обычном; в случае спина 1/2 ортогональные состояния |↑〉 и |↓〉 представляют физические конфигурации, ориентированные, скорее, в противоположных направлениях, нежели под прямым углом.) Следующий пример — состояния |↑↑…↑〉, |↓↑…↑〉, …, |↓↓…↓〉 спина 1/2 n; каждое такое состояние ортогонально всем остальным. Ортогональными являются и все различные возможные положения, в которых может находиться квантовая частица. Более того, ортогональны как состояния |B〉 и i|C〉 (см. §5.7 — прошедшая и отраженная части состояния фотона, получаемые в результате падения фотона на полупрозрачное зеркало), так и состояния i|D〉 и —|E〉, в которые эволюционируют первые два после отражения от двух непрозрачных зеркал.
Последний факт иллюстрирует одно важное свойство шрёдингеровой эволюции U. Любые два изначально ортогональных состояния ортогональными и остаются, если каждое эволюционирует в соответствии с U в течение одного и того же временного периода. Таким образом, свойство ортогональности при эволюции U сохраняется. Кроме того, эволюция U сохраняет и значение скалярного произведения состояний. Собственно, именно в этом и заключается формальный смысл понятия унитарная эволюция.
Как уже упоминалось выше, ключевая роль ортогональности состоит в следующем: различные возможные квантовые состояния, возникающие при любом «измерении» квантовой системы и дающие — при поднятии на классический уровень — непосредственно различимые результаты, непременно ортогональны друг другу. Особенно наглядно это проявляется в нулевых измерениях — таких, например, как в задаче об испытании бомб, §§5.2 и 5.9. Не-обнаружение какого-либо квантового состояния устройством, способным это состояние обнаружить, приводит в конечном счете к тому, что результирующее состояние «перескакивает» в нечто, ортогонально противоположное тому состоянию, какое детектор, собственно, призван обнаруживать.
Как мы только что отметили, ортогональность математически выражается как обращение в нуль скалярного произведения состояний. Это скалярное произведение, в общем случае, представляет собой комплексное число, поставленное в соответствие какой-либо паре элементов гильбертова пространства. Если обозначить эти элементы (или состояния) через |ψ〉 и |φ〉, то упомянутое комплексное число записывается так: 〈ψ|φ〉. При этом выполняется ряд простых алгебраических тождеств, которые мы можем записать в следующем (несколько, правда, неуклюжем) виде:
〈ψ¯|¯φ〉 = 〈φ|ψ〉,
〈ψ|(|φ〉 + |χ〉) = 〈ψ|φ〉 + 〈ψ|χ〉,
(z〈ψ|)|φ〉 = z〈ψ|φ〉,
〈ψ|ψ〉 > 0, кроме случая |ψ〉 = 0.
Кроме того, можно показать, что 〈ψ|ψ〉 = 0 при |ψ〉 = 0. Мне не хочется надоедать читателю прочими математическими подробностями (если же таковые подробности кого-то заинтересуют, то ознакомиться с ними можно, открыв любой стандартный текст по квантовой теории; см., например, [94]).
Существенными для наших дальнейших нужд свойствами скалярного произведения являются лишь следующие два (уже, впрочем, упоминавшиеся выше):
векторы |ψ〉 и |φ〉 ортогональны тогда и только тогда, когда 〈ψ|φ〉 = 0,
произведение 〈ψ|ψ〉 есть квадрат длины вектора |ψ〉.
Отметим, что отношение ортогональности является симметричным (поскольку 〈ψ¯|¯φ〉 = 〈φ|ψ〉). Более того, произведение 〈ψ|ψ〉 всегда представляет собой неотрицательное вещественное число, из какового числа легко извлекается неотрицательный квадратный корень, который мы можем называть длиной (или величиной) вектора |ψ〉.
Поскольку при умножении любого вектора состояния на ненулевое комплексное число физическая интерпретация этого вектора никаких изменений не претерпевает, мы всегда можем нормировать состояние таким образом, чтобы длина соответствующего вектора стала равна единице, получив в результате так называемый единичный вектор, или нормированное состояние. Тут, впрочем, имеется некоторая неясность, так как мы можем умножить вектор состояния и на чистую фазу (число вида eiθ, где θ — вещественное число; см. §5.10).












