ЧАСТЬ III ПРАКТИЧЕСКАЯ ИНТУИЦИЯ

ГЛАВА 12 ИНТУИЦИЯ ИГРОКОВ

Почему люди играют в азартные игры?

Итак, у нас есть по крайней мере две группы игроков — дисциплинированные игроки, предающиеся азартным играм как виду отдыха и лишенные иллюзий относительно возможности выигрыша в долгосрочной перспективе, и люди с проблемой игровой зависимости, чьи ошибочные интуитивные предположения ведут к краху. Но в обоих случаях азартные игры тянут деньги из игроков. Лотерейный билет ценой в $1 имеет «ожидаемую ценность» всего лишь в 50 центов (поскольку штат выплачивает в виде премии лишь половину того, что ставят люди). Итак, почему же такое огромное число людей цепляется за ложные надежды? Почему люди стоят по три часа в очереди за билетами лотереи «Powerball», предварительно проведя два часа за рулем и приезжая из соседних штатов? Почему некоторые покупатели настолько убеждены в том, что их игровой автомат вот-вот расплатится с ними сполна? Поэтому они даже не отлучаются в туалет по естественной надобности: команде уборщиков помещения приходится иметь дело с мочой в пластиковых стаканчиках для монет и лужами на полу, оставленными теми, кто не надел на себя подгузники для взрослых.

Дрожь азарта — это явно один из компонентов ответа на этот вопрос. Жадность — еще один мотивирующий фактор. Но, учитывая тот факт, что умный жадина никогда не заплатит S1 за то, что стоит 50 центов, мы должны смотреть глубже. Почему человек обманывается своей жадностью? Какие когнитивные вирусы заражают интуицию азартного игрока?

Неправильное восприятие вероятности. Лотереи — это не только налог на бедных, но и, по словам математика из Университета Депола Роджера Джоунса, это «налог на тех, у кого трудности с математикой». Трудно интуитивно оценивать очень неравные шансы. Попытайтесь объяснить, что означает вероятность 10 тысяч к одному баскетболисту-старшекласснику, пренебрегающему уроками и мечтающими о месте в «NBA».

Психологи исследовали «субъективную переоценку» невероятных событий. Те, кто делает ставки, «переоценивают шансы маловероятных, но очень благоприятных исходов», — отмечает статистик из Университета штата Айова Хэл Стерн. В одном из своих исследований он проанализировал ставки, сделанные на 38 047 лошадей в 3785 забегах Гонконгских бегов. Результаты данного анализа, равно как и другие похожие работы, показали, что публика склонна недооценивать вероятность того, что победит явный фаворит, и переоценивать успех тех лошадей, которые идут в конце списка. «Людская интуиция плохо работает с вероятностью», — замечает Стерн.

Да, иногда забег выигрывают «темные лошадки». Когда вышедший на пенсию электрик из Иллинойса Фрэнк Капаси потратил $5 на покупку билетов лотереи «Powerball» в 1998 г., на каждый из его пяти билетов была сделана ставка 80,1 миллиона к 1. Среди покупателей 138,5 миллиона билетов — вследствие чего должны были выиграть один или два человека — Капаси стал единственным счастливым победителем, выигравшим $195 миллионов (на самом деле, после выплаты всех налогов, он единовременно получил $70 миллионов). Два месяца спустя 13 рабочих со сборочного конвейера в Огайо скинулись по $ 10 и приобрели 130 билетов. Они оказались единственными выигравшими — среди приобретенных почти 211 миллионов билетов — и выиграл и $295,7 миллиона в эту же лотерею. Через 9 месяцев в Бостоне Мария Грассо, эмигрантка из Чили, которая днем работала бебиситером, а по ночам ухаживала за детьми-инвалидами, купила три билета лотереи «Big Game». Один из этих билетов оказался единственным выигрышным среди проданных 83 миллионов билетов, и бывшая чилийка выиграла $197 (опять-таки, после уплаты всех налогов на руки она получила всего лишь $70 миллионов).

Три билета выиграли и произвели фурор. Однако более миллиарда проигравших билетов остались незамеченными на фоне этих трех джекпотов. (Каждый из этих выигрышей получили, как мы и ожидали, именно те люди, которым нравятся лотереи, — те, кто испытывал острую необходимость в деньгах, но кто не мог себе позволить никаких игорных долгов). Фантазии по поводу выигрыша кружат голову сорокадвухлетнему нью-йоркскому водителю грузовика Джо, который тратит на билеты лото еженедельно от $30 до $50. Хотя за четыре года он не выиграл ни цента — спустил за это время в надежде на джекпот $10 тысяч, — он упорствует в своих намерениях. «Ну, никогда не знаешь наверняка».

Да, вы действительно никогда не знаете заранее. Подумайте о тех тысячах исполненных надеждами людей, которым звонит «премиальный патруль» банковской расчетной палаты, вручающий призы, и говорит, что до их дома «трудно добраться» и что они их ждут в ресторане «Uncle Jack's». Это правда, никогда не знаешь наверняка. Но, учитывая то, что вероятность выиграть гран-при в $10 миллионов составляет 1:100 миллионам, возможно, они могли бы спокойно посетить этот дорогой ресторан и так. Мы осознаем шансы 1:100 или 1:1000, но различие между 1:10 тысяч и 1:80 миллионам или 1:100 миллионам вызывает путаницу в нашем сознании. Если вероятность выигрыша всего лишь 2:10 тысячам, то ставки могут показаться невероятно «тощими». Но не теряйте надежды — даже 1:10 тысячам дает вам шанс в 80 тысяч раз больше, чем билет лотереи «Powerball».

Молния все равно куда-нибудь попадет (однако молния с гораздо большей вероятностью попадет в вас, чем вы выиграете в лотерею «Powerball»). Да, странные вещи случаются. Для Марии Грассо выигрыш был невероятным счастливым случаем. В 1999 г. пассажиры сербского поезда, а через три недели пассажиры автобуса в Косово стали жертвами столь же невероятного несчастного случая. И поезд, и автобус ехали по мосту как раз в тот самый момент, когда бомбы НАТО поразили их. Такое стечение обстоятельств поистине невероятно. Но сбросьте достаточное количество бомб (или купите достаточное количество билетов), и кто-нибудь обязательно погибнет (или получит приз).

Если, несмотря на все капризы судьбы, вы все-таки продолжите играть в лотерею «Powerball», есть одна умная вещь, которую вы можете сделать, например так, как три упомянутых выше победителя, и выберите те номера, на которые не поставят другие, кто разделил бы с вами приз в случае выигрыша. Учитывая, что любая комбинация из пяти случайных чисел от 1 до 49 так же вероятна, как любая другая, не выбирайте свои числа так, как, по мнению большинства людей, должна выглядеть случайная последовательность (скажем, 3,17, 25,32 и 46). В выигравшем билете «чертовой дюжины счастливчиков из Огайо», четыре числа приходились на интервал от 39 до 49. В 2001 г. Кармен Кастеллано, вышедшая на пенсию клерк из супермаркета в г. Сан-Хосе, штат Калифорния, стала единственным победителем «Superlotto» и выиграла $141 миллион, выбрав номера 3,22,43, 44,45 (и меганомер 8).

Психолог Эйлин Хилл отмечает такое же явление в Британской национальной лотерее, в которой люди должны выбрать 6 номеров из 49. В те дни недели, когда не бывает победителей, выигрывают обычно последовательности, которые не выглядят случайными, например, такая: 2,5,21,22,25,32; недели, когда наблюдается множество победителей, обычно характеризуются отсутствием сочетаний элементов и числами, далеко отстоящими друг от друга, — именно этого многие люди ожидают от случайных данных. Во время одной из лотерей, когда выиграла последовательность 1,17,23,32,38 и 42, оказалось 133 победителя, которые поделили между собой выигрыш. Ирония ситуации состоит в том, что большинство людей, которые пытались генерировать последовательность, которая выглядела бы случайной, забывают о сочетаниях элементов, которые так часто наблюдаются в случайных данных. И когда они придумывают последовательности, им зачастую не хватает изобретательности. Последовательность 1,2,3,4,5 и 6 так же вероятна, как любая другая. Но почти 30 тысяч игроков среди 128 миллионов покупателей билетов выбрали именно ее. Хотя нет лучше способа составить случайную последовательность чисел, чем позволить машине сделать это за вас, многие люди думают, что они справятся с этим лучше.

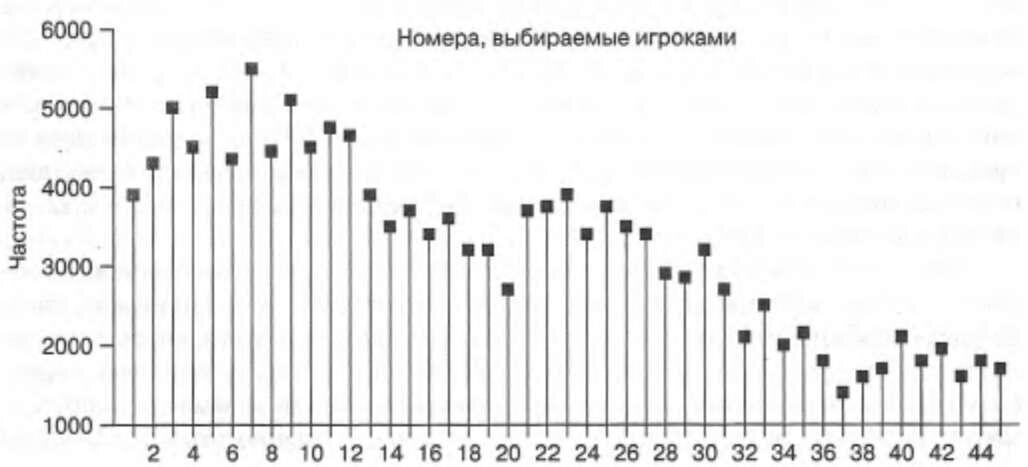
Есть еще одно распространенное неслучайное предпочтение в отношении чисел, представляющих собой даты рождения. Чтобы объяснить это предпочтение, исследовательница из Дартмура Лори Снелл исследовала 102 006 чисел, выбранных 17 001 человеком в лотерее «Powerbal» в 1996 г., где надо было выбрать числа от 1 до 45. Как показано на рисунке, меньшие числа, связанные с днями рождения (и счастливыми номерами), на самом деле были более вероятными. Самым популярным числом была семерка; менее одной трети тех, кто выбрал семерку, выбрали наименее популярное число 37. Юбилейный тираж Британской национальной лотереи отдал предпочтение маленьким номерам — 5 из 6 были меньше 31 (нужно было выбирать из 49 чисел). В результате бывало так, что джекпот делили между собой семеро победителей. Поэтому, чтобы не делиться выигрышем, не выбирайте популярные номера.

Психологи Томас Хольтгрейвс и Джеймс Скил исследовали то, как люди воспринимают случайность, на примере лотереи «Выбери 3 числа» штата Индиана. Вы тоже можете сыграть: выберите любое трехзначное число от 0 до 999.

Есть ли в вашем числе повторяющиеся цифры (как, например, в 737)? Возможно, нет. Только 14% из 2,24 миллиона числовых последовательностей, выбранных в июле 1991 г., имели повторяющиеся цифры. Хотя на самом деле повторяющиеся цифры присутствуют в 28% существующих чисел, такие числа выглядят менее случайными (а люди предпочитают серии цифр, выглядящие случайными). В настоящих случайных последовательностях, как мы отмечали в главе 7, кажущиеся паттерны и сочетания элементов (например, повторяющиеся цифры) встречаются гораздо чаще, чем думают люди.

Можно также нажиться на ошибочной интуиции других людей, поставив на те номера, которые только что выиграли. В одной из работ, анализирующих ставки, сделанные в течение 12 недель на лотерею «Выбери 3 числа» штата Мериленд, выигрышным номерам потребовалось 3 месяца на то, чтобы восстановить свою бытую популярность. Другая работа, содержащая анализ данных по 1785 ежедневным розыгрышам лотереи «Выбери 3 числа» в штате Нью-Джерси, показала, что на числа, выигравшие в предыдущем розыгрыше, ставило на 25% людей меньше. Это желание «делать ставку на числа, которые должны выиграть» и избегать чисел, которые оказались выигрышными незадолго до этого, — «заблуждение игрока» — великолепный пример для аудитории. Я кидаю монетку, но перед каждым броском я предлагаю студентам записать их предсказание — орел или решка. Я объявляю итог: орел, решка, решка, решка, решка Затем, перед шестым броском, я говорю: «Поскольку существует вероятность 50 на 50 как для орла так и для решки, половина из вас предскажет каждый из этих результатов, правильно?» Однако подавляющее большинство предсказывает выпадение орла — как если бы отсутствие орлов до этого момента как-то могло повлиять на результат следующего броска.

Заблуждения игрока питают интуицию игрока. «Мне должно повезти». «Скоро шансы изменятся в мою пользу». Да, это правда, за исключительным невезением, скорее всего, последуют не столь сокрушительные неудачи (поскольку случайным образом варьирующиеся результаты склонны стремиться от крайностей к среднему). Томас Гилович отмечает, что если вы проиграли 4 раза подряд в рулетку, то существует 95%-ная вероятность того, что во время следующих четырех поворотов рулеточного колеса вам повезет больше. Но это происходит отнюдь не вследствие некоего автоматического процесса самокорректировки: ваши шансы выиграть остались точно такими же, даже если бы вы выиграли во время четырех предыдущих поворотов колеса У монет, колеса рулетки и лотереи память отсутствует!

Статистик Рума Фальк приводит великолепную параллель. Задумайтесь на минутку: правда ли, что у мужчин больше сестер, чем у женщин?

Большинство студентов Еврейского университета в Иерусалиме, изучающие теорию вероятности, сказали, что это правда Фальк отмечает, что «интуитивно это утверждение может показаться истинным, потому что "в среднем" в семье одинаковое число сыновей и дочерей»; средняя семья стремится завести девочку, чтобы уравновесить присутствие брата. Но это сродни заблуждениям игрока. Пол первого родившегося ребенка не влияет на пол остальных детей в семье. В момент зачатия яйцеклетка и сперматозоид не знают, дети какого пола были зачаты ранее. В семьях с двумя детьми есть четыре равновероятных «набора» потомства: мальчик, мальчик; мальчик, девочка; девочка, мальчик; и девочка, девочка. Заметьте, что половина детей в этих семьях имеет сиблинга²⁴ одного пола с собой, а половина — сиблинга противоположного пола. Это же справедливо и для семей с большим количеством детей. Поэтому на вопрос Румы Фалька следует дать отрицательный ответ: у мужчин столько же сестер, сколько у женщин.

²⁴ Сиблинг — брат или сестра. — Примеч. науч. ред.

Иллюзия контроля. Ошибочное восприятие вероятности — не единственный вирус, поражающий интуицию азартных игроков. Психолог из Гарвардского университета Эллен Лангер продемонстрировала наличие «иллюзии контроля» в экспериментах с азартными играми. По сравнению с теми, кто получал номер, выпавший им в лотерее, те, кто сами выбирали номера, требовали в 4 раза больше денег, если их просили продать их билет. Играя в азартную игру с неловким и нервным человеком, они делали гораздо более высокие ставки, чем играя с элегантным, уверенным в себе противником. Самостоятельно выбрасывая кости для себя, они чувствовали себя более уверенными, чем когда это делал за них крупье. Если у них была возможность попрактиковаться, то их уверенность возрастала. Таким образом, более чем в 50 экспериментах было показано, что люди действовали так, как будто могли предсказывать или контролировать случайные события.

Наблюдения за игроками в реальной жизни подтвердили результаты этих экспериментов. Игроки в кости могли бесшумно кидать кости, если речь шла о маленьких номерах, и делать это с грохотом — если о больших. Чтобы подманить счастье, они дули на кости, концентрировались на нужном числе, перекладывали кости в левую руку или вставали и обходили вокруг стула 3 раза. Индустрия азартных игр процветает за счет иллюзий игроков. Игроки приписывают свои выигрыши своему умению и прозорливости. Проигрыши становятся «попаданиями около цели» или «случайностями», связанными, возможно (в случае участников спортивных тотализаторов), с несправедливым судейством или капризом полета мяча. Сэмюэль Джонсон, английский мудрец XVIII в., размышляя об иллюзиях интуиции, назвал лотереи «налогом на дураков».

Запоминающиеся победители. Начиная с казино и заканчивая лотереями штатов, проигравшие остаются за кадром, тогда как на победителей направлен яркий свет софитов. Казино с шумом и помпой объявляют даже о незначительных выигрышах, превращая их в запоминающиеся события, тогда как о проигрышах скромно умалчивают. Наши собственные выигрыши также более заметные и запоминающиеся события, подобно тому, как мы запоминаем те рыбалки, когда мы поймали рыбу, а не те, когда у нас не клевало. Это помогает объяснить результаты, полученные в 1999 г. Национальным центром исследований общественного мнения: азартные игроки Америки считают, что они выиграли в казино на $4 миллиарда больше, чем протирали, тогда как на самом деле они оставили там на $20 миллиардов больше.

«Люди, получающие главные призы в лотереях, — Фрэнк Капаси, Мария Грассо» и «Счастливая чертова дюжина», — это передовицы в газетах и новости в прайм-тайме. Эти живые примеры легко приходят нам на ум, а. как мы знаем, «когнитивная доступность» — это главное правило интуитивных предположений относительно частоты событий. После того как Фрэнк Капаси выиграл $195 миллионов в лотерею ($ 104 миллиона после уплаты налогов), одна женщина из Канзаса пожаловалась Энн Ландерс, что ее муж, страстный игрок в лотерею, заявил ей: «Смотри, молния действительно ударяет. Это мог бы быть я». — «Да, Джим, — ответила жена. — Это мог бы быть ты, но это — не ты».